Projects
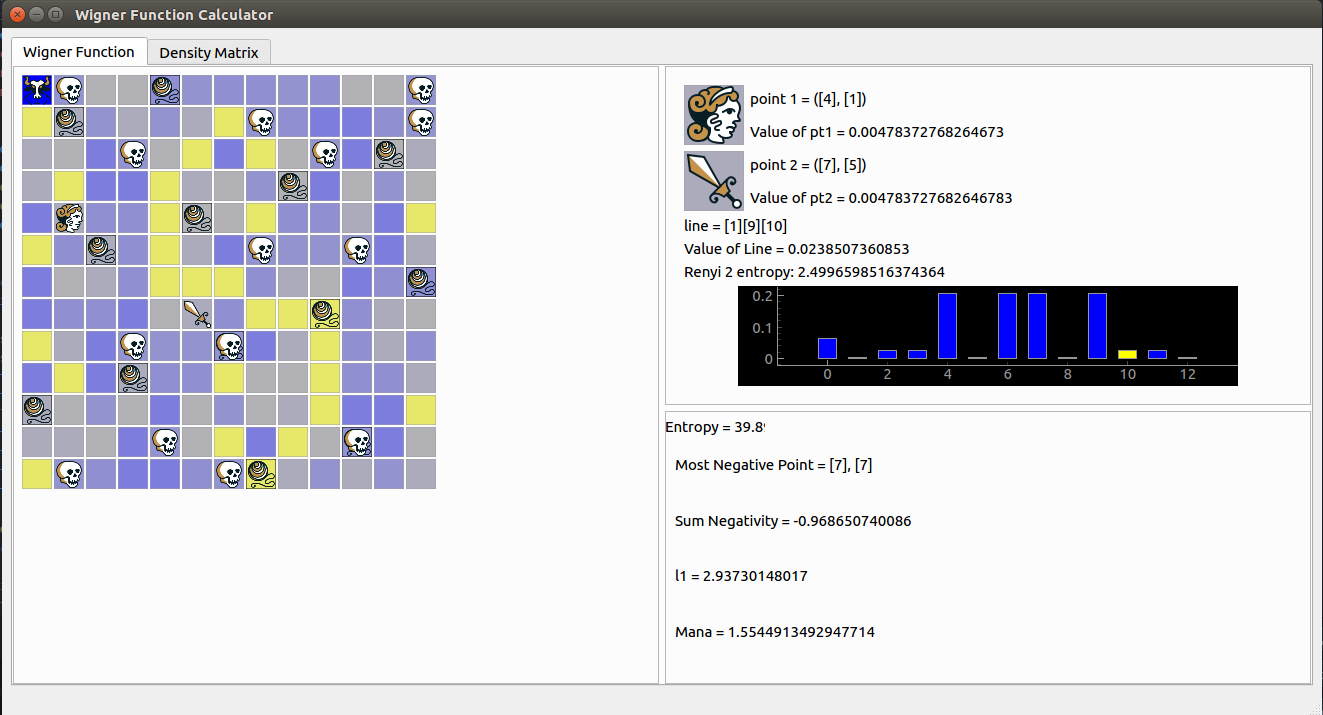
I've been working on a calculator for the Wigner function to assist me with various computations. Here is a link to the code.
To predict the behavior of complex systems, like nested pendulums, it is nice to work in phase space, where the position and momentum of each degree of freedom are plotted. This is called Hamiltonian mechanics. Wigner adapted the phase-space picture to the quantum case. There is an added complication that position and momentum cannot be determined simultaneously. Wigner devised a scheme to introduce negative probabilities so that the phase space picture would agree with any measurement that could be performed. The techniques appear to come from harmonic analysis.
Wigner's work applied only to infinite-dimensional systems, but in the context of quantum information, it is more natural to work with finite-dimensional systems. David Gross adapted Wigner's function to the odd finite-dimensional case, and convicingly argued that this function is unique.
I wrote a python program that calculate the Wigner function, with an emphasis on states of prime power dimension, considered as single-particle systems. The program can calculate minimum-uncertainty states for odd-prime dimensions which are 3 mod 4, and can interconvert unitary and affine transformations.
My old project was a multidimensional Tic-Tac-Toe game written in Javascript.
It was lots of fun to write. I gave the positions addresses, along with a function from the addresses to the numbers 1 .. #positions, based on base-9 arithmetic. By positions, I don't just mean the 81 places you can play, but the 81+9+1=91 groupings of buttons. Interestingly, if you index starting at 0, you'll run into a problem: The top left square's address is [0,0,0], the bigger top left square's address is [0,0], and the whole board has address [0]. These all 0 when interpreted as base-9 numbers! For this project, I found it more convenient to label starting with 1.
The other fun part about this project was devising the strategy for the ai. One wins at tic-tac-toe by capturing a line. This means that you should judge your position based on how many lines you control. On the outer 3x3 board, the individual squares themselves are boards, so players might have partial control over the squares. The partial control ought to be calculated recursively, so that control over the squares is calculated in the same way as control over the whole board. Thus, a strategy is determined by how much to value 1 on a line and how much to value 2 on a line, then propagating these calculations upward to determine who is winning the biggest board and by how much. You can put some simple bounds on these two parameters and attain a class of strategies, and the one implemented in the code is chosen as a midpoint. This analysis leaves out certain things, such as that 2 partial lines which are completed by the same square is less valuable than 2 partial lines completed by different squares.
Description
- Players X and O (gold and silver) take turns marking squares
- A player can only play on the allowed board (purple), which is determined by the previous moves
- A player captures a board by getting 3 in a row. If the other player gets 2 sets of 3 in a row, he may steal the board.
- The game is won when the largest board is captured.
- If a player is forced to play on a full board he/she may play anywhere within the larger board containing this full board.
- The Toggle Size button creates a new game with a different size.
- The Add Bot creates a bot which uses alpha beta/pruning with a depth search up to 5.
- You can press the Add Bot button again to see the bot play itself. (this takes a little while on the largest board)
- For some reason, this doesn't work on mobile. Possibly due to CSS grid?
- The Undo Move button undoes the last move. If you are playing a bot, you'll have to click it twice to undo the bot's move and your last move.
- Through development, the undo move button has been buggy. It had better work now, because the bot relies on this function.